Categorical Syllogism
A GLIMPSE INTO THE DEPTHS
Categorical syllogism is an ancient, yet still
extremely useful, form of deductive reasoning. We've already
taken a cursory look at an ages-old example, to consider how each of its
three statements links to the other two.
All men are
mortal.
Socrates is a
man.
So, Socrates is
mortal.
In this lesson, we'll examine the parts,
structure, and function in greater detail. Again, we'll be
breaking the statements into subject and predicate components, but this
time we'll carry the analysis a bit further. The purpose of
this exercise is not to lead the reader to believe that Socrates died
from boredom, but to acquire a firmer grasp of precisely how logical
argumentation works. With such knowledge, we can then figure out
how categorical arguments can (and cannot) be legitimately formulated
and interpreted.
Subject and predicate
Syllogisms can take a variety of forms. But the
classic categorical syllogism is marked by a specific, compact,
well-defined form, and therefore serves as a very handy model for the
study of reasoning in general. To begin, we note that the classic
form has
exactly three statements: two premises—All men are mortal and
Socrates is a man—and one conclusion—Socrates is mortal.
Terms
of a syllogism As we learned before, each statement comprises a subject
and a predicate. The subject and predicate each contain one
term of the syllogism, thus each statement poses a
relationship between two terms..
- In the first statement of our example, men is the
subject term, and mortal is the predicate term.
- In the second statement, Socrates is the subject
term, and a man is the predicate term.
- In the third, Socrates is again the
subject term, and mortal is the predicate term.
Thus, the classic categorical syllogism contains
three terms (in this case man / men, mortal, and
Socrates). Each of the three statements of the syllogism
contains two of these three terms. The conclusion's predicate term
(mortal) is called the major term
of the syllogism, and the conclusion's subject term (Socrates) is
called the minor term of the
syllogism. The remaining term (man / men), which is
not found in the conclusion, but (in this case) is the subject term of
the first premise and the predicate term of the second premise, is
called the middle term of the
syllogism.
Working from this, we can further differentiate
the syllogism's two premises. The premise whose predicate term is
the same as the syllogism's major term (mortal) is identified as
the major premise. The other
premise, then, becomes the minor premise
of the the syllogism.
Sequence of statements
As far as logic goes, the statements of a syllogism
can be arranged in any order—
major premise, minor premise, conclusion (All
men are mortal [and] Socrates is a man, [so] Socrates is mortal);
minor premise, major premise, conclusion (Socrates
is a man [and] all men are mortal, [so] Socrates is mortal);
major premise, conclusion, minor premise (All
men are mortal, [and] Socrates is mortal, [because] Socrates is a man);
minor premise, conclusion, major premise (Socrates
is a man, [and] Socrates is mortal, [because] all men are mortal);
conclusion, major premise, minor premise (Socrates
is mortal, [because] all men are mortal [and] Socrates is a man);
conclusion, minor premise, major premise (Socrates
is mortal, [because] Socrates is a man [and] all men are mortal)
—and the sequence makes no functional difference as to the reasoning.
However, to avoid confusion in the study process, it's customary always
to place the major premise first, the minor premise second, and the
conclusion last.
With the statements arranged in the standard
order, it's easy to detect the linkages among them. And we can
further illustrate these linkages by representing the various terms
visually.
In the major premise, All men are
mortal, all things belonging to the category specified by the middle
term men is determined also to be included in the category
defined by the major term as [things that are] mortal. If
we represent the category of men as a circle, and the larger
category of things that are mortal as a square, we show that the
first is contained within the second, thus:
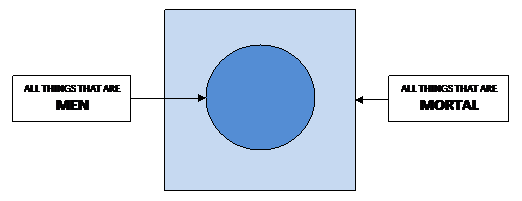
The minor premise, Socrates is a man,
signifies that the single thing in the category identified by the minor
term Socrates is included within the category of the middle term
men. If we continue to use the circle to represent the
category of men, and represent the category of things that are
Socrates as a single dot, we can illustrate the relationship described
in this premise thus:
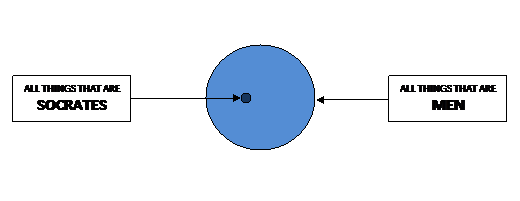
We obtain the conclusion, Socrates is mortal,
by combining the information provided in the two premises. When we
do this, we can then bypass the middle term, men, which has already
served its purpose by providing the logical link between the major and
minor terms. In this way, we're able to conclude that the category
of the minor term Socrates is entirely contained within the
category of the major term [things that are] mortal.
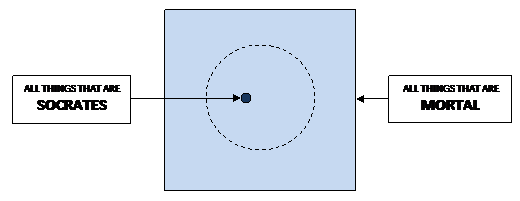
Using classical categorical syllogism as a well
developed example, we're now beginning to see and appreciate how some of
the logical relationships and connections we routinely take for granted
actually work to hold reasoning solidly together.
▼