|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
The Square of Opposition
The four forms of categorical
statements would appear, even at a casual glance, to have some implicit
interrelationships in play among them. The relationships are
defined by two opposed sets of qualities: universality versus
particularity, and affirmation versus negation.
|
Form |
|
Relationship |
|
Structure (Plural) |
|
|
|
Structure (Singular) |
|
A |
|
universal |
|
affirmative |
|
All S are
P |
|
or |
|
Every S is
P |
|
E |
|
universal |
|
negative |
|
No S are
P |
|
or |
|
No S is
P |
|
I |
|
particular |
|
affirmative |
|
Some S are
P |
|
or |
|
At least one S is
P |
|
O |
|
particular |
|
negative |
|
Some S are not
P |
|
or |
|
At least one S is not
P |
Aristotle (384-322
bce), the Greek philosopher
credited with organizing principles of rational thinking into a clear and methodical
system of rules, devised a conceptual diagram to illustrate the interactions
among categorical relationships. As an exercise in learning by
doing, let's attempt to duplicate his process of developing the classic
square of opposition.
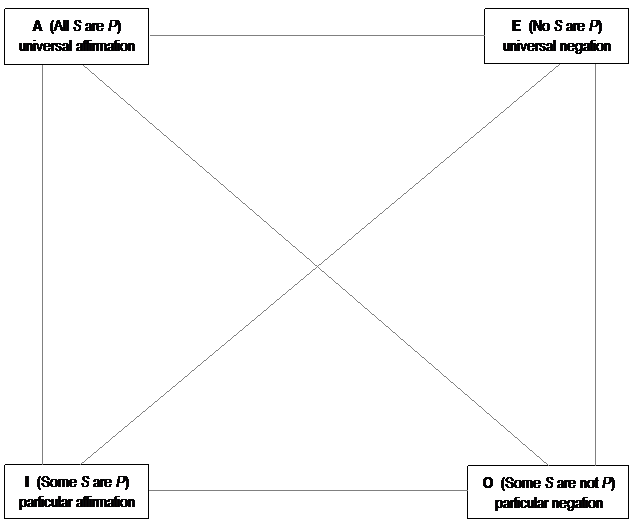
THE BASIC SQUARE
If we arrange the four
relationships as the four corners of a square, we should be able to
illustrate those opposing forces, and analyze the implications between
each pair of relationships. We'll begin by laying out the square
with universal forms at the top and particular forms at the bottom, and with
affirmations to the left and negations to the right. Then we'll
indicate all possible interconnections with a line drawn between each
pairing of forms.
Next, we'll identify the
interactions between each pair of relationships, and use symbolic
notation to describe them. In assessing the compatibility of each
pair of relationships, we need to answer the following four questions:
1. Is it possible for both
relationships to be simultaneously true?
2. Is it possible for both
relationships to be simultaneously false?
3. Is it possible for either
relationship to be true when the other is false?
4. Is is possible for either
relationship to be false when the other is true?
Once we've determined the answers
to these questions, we can identify the logical pattern that it follows,
and use standard symbolic notation to express it.
▼
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
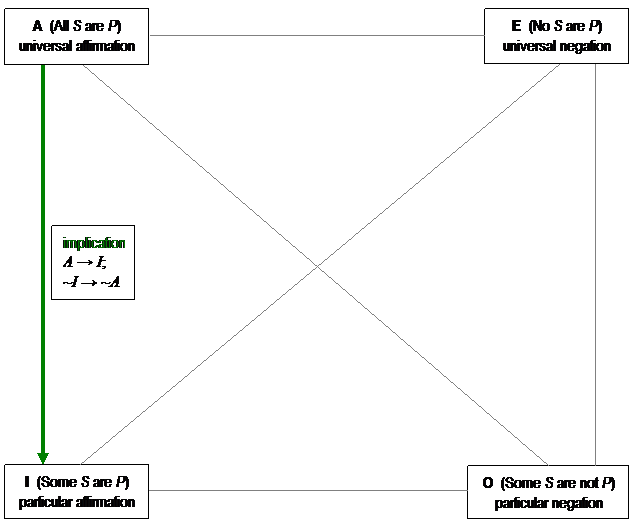
THE AFFIRMATIONS: A
AND I
Our first comparison is between the
A statement, All S are P, and the I statement, Some S
are P. Now, a condition that applies to some S might
or might not apply to all S. But any condition that applies
to all S must apply to some S. In other words, if
some things in category S are also in category P,
this
tells us nothing about whether all S are P (e.g., some signs
are no-parking signs does not imply all signs are no-parking
signs); but if all things in
category S are also in category P (e.g., all squids are predators), then we can be certain that
some S
are P (some squids are predators) So we get the following pattern of answers:
1. It's possible for both A and I to
be true, because I must be true whenever A is true.
2. It's possible for both A and I to be false, because A must be false
whenever I is false.
3. It's possible for A to be false
when I is true, because some does not imply all.
4. It's impossible for A to be true
when I is false, because all implies some.
The pattern is such that whenever A
is true, it's implied that I must also be true. This
pattern corresponds exactly to the logic of IF A THEN I,
or in symbolic notation, A → I.
Furthermore, a false value for I implies that A
must also be false. And indeed, this corresponds to the
contraposition of A → I,
which (as we learned in the Symbolic Logic section) is IF NOT I
THEN NOT A, or ~I → ~A,
which neatly confirms our assessment. Pairs of categorical
statements, the second of which must be true if the first is true, and
the first of which must thus be false if the second is false, are called
implications. An implication
is a condition that works in one direction only; that is, "all S
are P" implies "some S are P," but "some S
are P" does not imply "all S are P."
▼
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
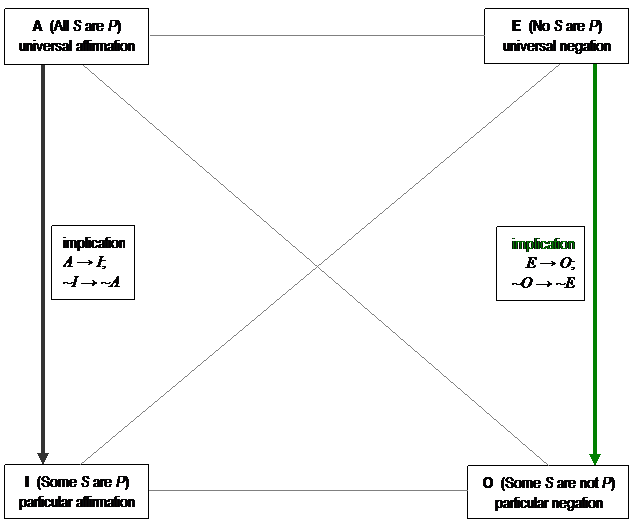
THE NEGATIONS: E
AND O
Although we're here dealing with
negations rather than affirmations, the same principle holds: A
condition that applies to some S might or might not apply to all
S, but any condition that applies to all S must also apply
to some S. Thus, we get a similar pattern of answers to our
four questions:
1. It's possible for both E and O to
be true, because O must be true whenever E is true.
2. It's possible for both E and O to
be false, because E must be false whenever O is false.
3. It's possible for E to be false when O is true, because some does not
imply all.
4. It's impossible for E to be true
when O is false, because all implies some.
And again, this pattern corresponds
to the conditional relation, E → O,
and is confirmed by its contraposition, ~O → ~E.
Again, these relationships are implications, and are thus
one-directional: "No S are P" implies "some S are
not P," but "some S are not P" does not imply "no
S are P."
▼
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
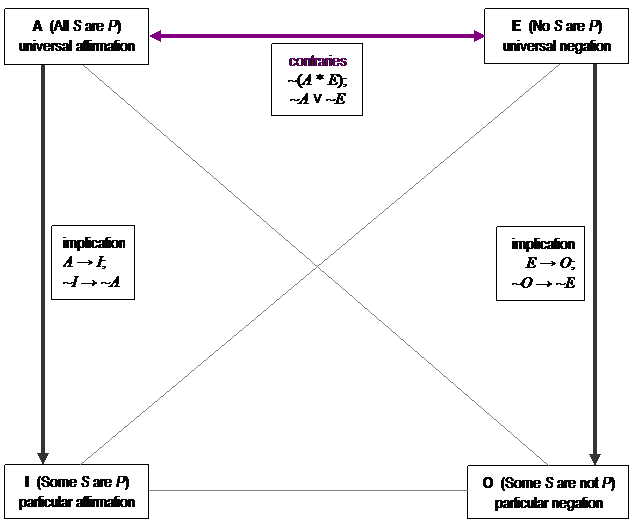
THE UNIVERSALS: A
AND E
The universal forms are represented by
statement A, All S are P, and statement E, No S are
P. When all of category S is contained in category P, then
there can be nothing in category S that is outside category P.
Likewise, if all of S is outside category P, then there can be none of S
inside category P. In this situation, the only impossible
configuration is that both statements A and E are true; all situations
in which one or both statements are false are possible.
1. It's impossible for both A and E to
be true, because the two statements are mutually exclusive.
2. It's possible for both A and E to
be false.
3. A must be false whenever E is true.
4. E must be false whenever A is true.
This pattern corresponds to the
logical negation of the conjunction of statements A and E, expressed as
NOT (A AND E), or symbolically as ~(A * E). Pairs of
categorical statements, at least one of which must be false, are called
contraries.
▼
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
THE PARTICULARS: I
AND O
Here we are dealing with statement
form
I, "Some S are P," and statement form O, "Some S are not
P." Obviously, it's possible for some of S to be in
category P while some other S is outside category P.
It's also possible for some (all) of S to be within category P while
none of S is outside P, or for some of S to be outside P when there is
no S inside P. The only impossibility is for all of S to be
both entirely inside and entirely outside category P at the same
time.
1. It's possible for both I and O to
be true.
2. It's impossible for both I and O to
be false, because there's no S that both is and isn't P.
3. It's possible for E to be false
when O is true.
4. It's possible for O to be false
when E is true.
Pairs of categorical statements, at
least one of which must be true, are called
subcontraries.
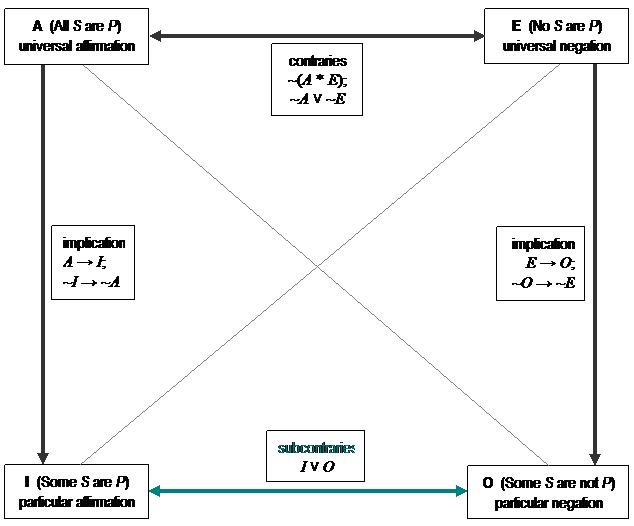
▼
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
THE OPPOSING CORNERS: A
AND O, E AND I
The statements, "All S are
P" and "Some S are not P," directly contradict each
other. Likewise, the two statements, "No S are P" and
"Some S are P" are mutually contradictory. It is
logically impossible for two mutually contradictory statements to have
the same truth value; one must be true, and the other most be false.
1. It's impossible for both A and O to
be true, and impossible for both E and I to be true.
2. It's impossible for both A and O to
be false, and impossible for both E and I to be false.
3. A must be true when O is false, and
vice versa.
4. E must be true when I is false, and
vice versa.
This pattern illustrates an
exclusive disjunction, "either one option or the other, but not both,
and not neither." As we saw in the Symbolic Logic section, this
pattern is succinctly expressed as the negation of a bi-condition, in
these cases ~(A
↔ O) and ~(E
↔ I). Pairs of categorical statements,
the truth values of which must always be opposite, are mutually
contradictory. Contradictories
illustrate the exclusive OR (XOR) relationship, which we briefly
discussed in symbolic logic, and which can be symbolically expressed as
the negation of a bi-condition. The truth values of contradictory
statements must be opposite to each other; if one is true, then the
other must be false, and vice versa.
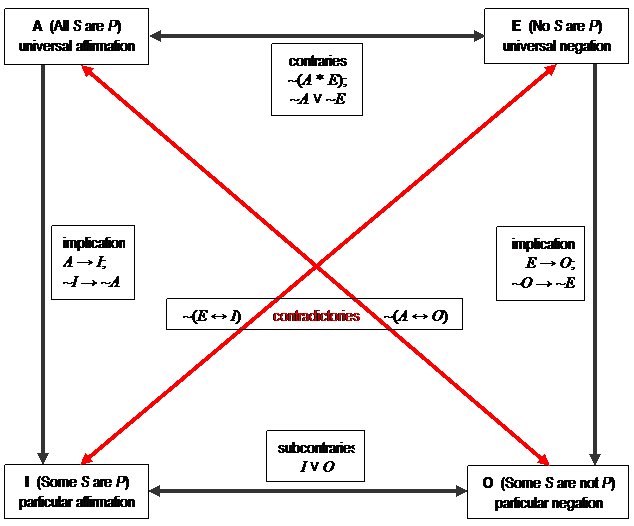
▼
|
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |
THE CLASSIC SQUARE OF
OPPOSITION
We've now explored all possible
pairings of the four categorical statement types. If these
relationships did not seem commonsense before, they should after having
considered the reasoning behind them. If they still aren't burned
into your psyche, you might want to make a copy of our pretty square and
review it until it becomes second nature, because the relationships it
illustrates are a very fundamental part of reasoning. Once you
fully understand it, you're not likely to forget it—or if you do, it
shouldn't require much effort to figure out again.
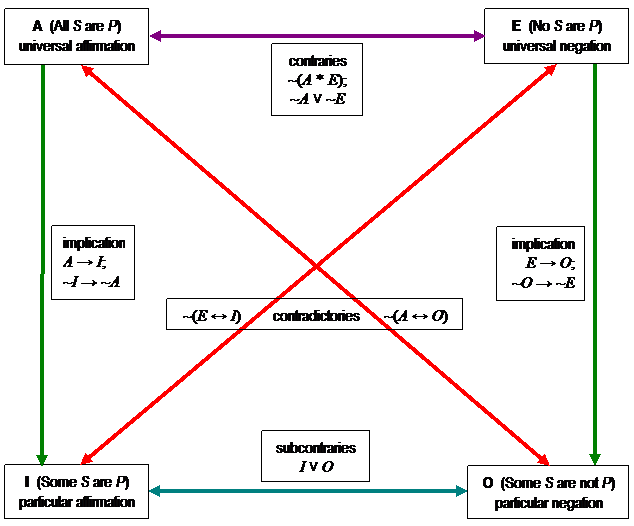
Aristotle's principles of reasoning held
firm, essentially unchanged and unchallenged, for nearly two and a half
millennia.
By the 18th century, this impressive record of durability had long been
considered convincing
evidence that his system of logic was perfect and could not be improved upon.
Relatively recently, though, a few adjustments have been made as a
result of an explosion of intellectual innovation in the modern era.
THE MODERN SQUARE OF OPPOSITION
One of these latter-day tweaks derives from the mathematical concept of
zero, which didn't
exist in Aristotle's time and culture. The ancient view was that,
if a category contained nothing at all, then the category itself didn't
exist. Modern thinking, though, considers categories as concepts, rather
than as collections of actual things. To speak metaphorically,
even if there isn't a molecule of tea in it, the teapot itself still
exists. This shift in thinking has the following effect on
categorical reasoning. Consider: If the current number of humans
on our planet is seven billion, then "all humans now alive" equates to
"seven billion humans." And if the number of planets inhabited by
humans is one, then "all planets inhabited by humans" equates to "one
human-inhabited planet." To follow the same pattern of thought, if
the number of humans on the surface of Venus is zero, then "all humans
on Venus" equates to "no humans on Venus." So, in an empty
category, "zero" is
equivalent to "all."
Under this condition, some of the
relationships in the classic square of opposition break down. When
any subject category S could conceivably be empty, then the
classic contraries "All S are P" and "No S are P"
are no longer mutually exclusive, for both become simultaneously true if
category S is empty. "All S are P" no longer
implies "Some S are P," and "No S are P" no
longer implies "Some S are not P," if there's a
possibility that there is no S. Even the subcontrary
relationship, that either "Some S are P" or "Some S
are not P" must be true, ceases to hold up if no S exists.
The only relationships left standing when category S is empty are
the contradictories: "All S are P" and "Some S are
not P" continue to have opposite truth values, as do "No S
are P" and "Some S are P." So, the modern
square of opposition boils down to this:
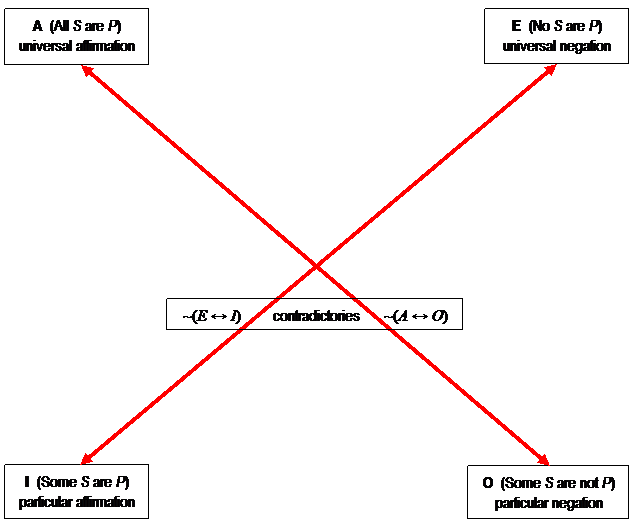
Now, it would be a mistake to
propose that the modern square of opposition renders the classic model
worthless. From a practical standpoint, in most real-world cases
concerning non-conjectural things, it's safe to assume that most subject
categories contain at least one actual example. And as long as the
subject category S isn't empty, then all of Aristotle's logical
relationships remain intact; we can rely on them. But we should be
aware of what happens in the special case when there's a significant
chance that the actual number of S could be zero. This is
especially important when S is something uncertain or
unverifiable, like phlogiston,* God-given rights, or hard-working
philosophers. We'll see the implications of this in the next
lesson.
*Phlogiston is a now
obsolete concept of a massless fluid once believed to be a component in
all flammable substances and released as heat and flame during
combustion.
▼
|
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS
|
TERMS
Click a term to review its definition or
explanation in the text.
Aristotle's thinking and his square of
opposition dominated the principles of logic until the 1800s.
Since then, however, innovation has devised new ways to express,
visualize, and evaluate logical concepts. In the next lesson,
we'll consider John Venn's eye-catching graphic approach to categorical
reasoning, and we'll experience visually how the possibility of an empty
category limits what we may legitimately infer from a line of reasoning.
=R4=
►
Next: Venn
Diagrams
|
|
BASIC SQUARE |
AFFIRMATIONS |
NEGATIONS |
UNIVERSALS |
PARTICULARS |
OPPOSING CORNERS |
COMPLETED SQUARE |
TERMS |







