WELCOME TO THE UNIVERSE! | USING A VENN DIAGRAM | ADDING ANOTHER CATEGORY | UNDISTRIBUTED MIDDLE FALLACY | TERMS

Venn Diagrams

WELCOME TO THE UNIVERSE!

Yes, this bit of abstract eye-candy is the universe, as conceptually divided into three overlapping categories (the three circles) of stuff, plus a fourth category—the white rectangle representing the whole universe—which contains those first three categories and everything in them, as well as anything else that doesn't belong in any of those three.

This is a universe of interrelated concepts, as depicted by British logician John Venn (1834-1923), arguably the best known force in the modern revolution of categorical logic and set theory, prior to the advent of computers.  Before Venn's innovation, operations in logic were almost entirely confined to dry text, obscure symbols, and tedious tables.  Venn's simple diagramming techniques instantly increase both the practical utility and the accessibility of logic.  By giving reason an easily executable and viewable dimension, Venn diagrams make once obscure categorical relationships both visually appealing and almost intuitively comprehensible.  Indeed, Venn-style diagrams have found wide application outside the field of logic, because they present even moderately complex information in a clear and attractive visual format.  We introduce these techniques here as an additional tool (or plaything) for understanding, using—and yes, even enjoying—critical thinking.

▼

USING A VENN DIAGRAM

We ought to begin with something fairly basic, so, for the time being, we'll reduce the number of circles to two.  The following diagram represents the universe (the rectangle) and two categories of things (the circles) with which we happen to be concerned.  Notice that the diagram comprises four distinct areas, which we can tentatively identify by color.  The blue area is the portion of the left circle that does not overlap another circle.  The red area is the portion of the right circle that does not overlap another circle.  The lens-shaped violet area is shared by the overlapping portions of the left and right circles.  And the white area is the portion of the universe that lies outside both circles.

As it stands, the diagram is otherwise blank.  (And in the next diagram we'll remove the area-identifying colors as well, which could otherwise prove confusing later.)  The lack of other marks in the diagram reflects that we don't yet know whether any of the four areas actually contains anything.

To address this, we need some information—likely in the form of a categorical statement, such as "Some Scandinavians are Protestants."  In this case, we identify each circle in the diagram with one of the two terms, "Scandinavians" being the subject term and "Protestants" being the predicate term of the statement.  The statement "Some Scandinavians are Protestants" indicates that the area where the categories of Scandinavians and Protestants overlap contains some (at least one) actual object (one or more Scandinavians who are also Protestants), so we place an x (called by most Venn users a "cross") in the area of overlap to mark it as occupied.

Now suppose we learn that some Scandinavians are not Protestants.  In this case, we want to indicate that something exists in a part of the category of Scandinavians that does not overlap the category of Protestants.

Obviously, we can combine these two pieces of information in a single diagram, simply by placing x's in both areas.  So we diagram "Some Scandinavians are Protestants, and some Scandinavians are not Protestants" thus:

"Well," one might interject, "we also know that there are Protestants who aren't Scandinavians.  So why don't we mark an x in the non-overlapping area of the P circle?"  It's a fair question.  The answer is that the diagram is supposed to represent a statement, not the whole of reality.  And in this instance, the statement we're considering—"Some Scandinavians are Protestants, and some Scandinavians are not Protestants"—makes no mention of non-Scandinavian Protestants.  Of course, if yet another statement tells us that "Some Protestants are not Scandinavians," then a composite diagram would indeed show an x in the unshared portion of the P circle.  Furthermore, if still another statement claims "Some non-Scandinavians are non-Protestants," then these individuals would be represented by an x somewhere in the rectangular universe outside both circles, since it represents something that exists but doesn't belong in either category.  Each x goes into the diagram only when a statement indicates in which area it belongs.

Now, note that each type of particular statement produces a characteristic pattern in a Venn diagram.  The identical patterns in the diagram above would appear for "Some scissors are made of plastic, and some scissors are not made of plastic," as well as for "Some people are women, and some people are not women."  (Although we may use any letters we like, in these examples we'll continue to use S and P to designate subject and predicate terms in general.)

Characteristic patterns apply to universal statements as well, but those patterns are noticeably different.  Universals present us with a different problem: how to indicate areas that are vacant.  Consider the universal negative statement "No spruces are pines."  Here we need to show, not in what categories the spruces are found, but where they are not to be found—which is to say, anywhere in the category of pines.  (Granted, spruces and pines may both physically grow in the same geographic area.  But still, no spruce is a pine, and no pine is a spruce.)  The statement claims that there's no categorical overlap between spruces and pines.  To indicate that the overlapping area in the diagram has nothing in it, we shade it out.

Universal affirmative statements are no more complicated to diagram; however, they require a little more explanation.  The statement "All swords are pointed objects" is diagrammed by showing that any part of the "swords" category that does not coincide with the "pointed objects" category is empty—again, by shading out every part of the "swords" circle that doesn't overlap the "pointed objects" circle.

What might seem odd is this: Even though we're told what all swords are, we don't place an x in the overlapping area.  This is because (according to modern thinking) an entire category can be empty—for example, the category of "flying unicorns."  Thus, "all flying unicorns" would equate to "zero flying unicorns" or "no flying unicorns."  Although we're pretty sure that, unlike flying unicorns, swords actually do exist, we must assume the possibility that they don't exist unless the statement indicates otherwise, for the purpose of the diagram is to illustrate graphically the conditions described in one or more statements, without adding anything not contained in the statements.  The reason for this will be addressed shortly, once we've dealt with the basics.

Now suppose we're considering two overlapping categories, one of sailors and one of pirates, and we're given only this statement as information: "Some sailors exist."  So, are all of these sailors pirates?  Or are none of the sailors pirates?  Are some of the sailors pirates and some not pirates?  The information provided doesn't offer a clue, so we don't know.  So, how do we diagram the statement?  Where do we mark the x?  In a case like this, we don't use an x.  Instead, we locate the border between the two areas where it's possible that the sailors exist (i.e., any border that passes through the "sailors" circle), and somewhere along this border we place a short, straight mark across it.

The cross-border mark means that one or both areas adjacent to the border are occupied.  In this case, we know from the statement that there are actual objects occupying some portion of the "sailors" category, but we can't be certain from the available information whether they're in the "sailors only" area or in the region that overlaps the "pirates" category—or perhaps are split up between the two areas.

Here's another pattern we might come across from time to time, exemplified by the statement, "All things that exist belong either to Spain or to Portugal."  The statement doesn't specify whether there's anything in one category or the other, in both, or in neither.  It does, however, state that all things that exist are in one or the other of these two categories, which means that nothing exists outside them.  We indicate this by shading out all parts of the universe that aren't in either of the category circles. 

But once more, the statement doesn't stipulate that the subject "all things that exist" actually contains anything, because the statement has neither explicitly stated nor implied that something belonging either to Spain or to Portugal does in fact exist.  This leaves open the possibility that the universe, and every category in it, is completely devoid of actual things.  Unless we get more information about which possibility is actually the case, according to modern thinking, we can't mark any of the categorized areas as either occupied or vacant, so we must leave them without marks or shading.  We can't even shade out the overlap between Spain's and Portugal's possessions, because the statement doesn't rule out the possibility that some things might be owned jointly by both countries.

But suppose we do get more information, in the form of two additional statements, which we receive in two separate postings a day apart.  The first statement informs us:
"To Spain belong some territories of the American continents and the Pacific Ocean west of the Line of Demarcation and east of the 180-degree meridian."
Now that we've learned that something actually belongs to Spain, we should mark this inside the S circle.  But the S circle is divided into two parts, the part overlapping the P circle and the part that does not overlap anything.  In which area do we put the mark?  The statement doesn't tell us, so we put a cross-border mark across the part of the P circle that passes through the S circle, to indicate that something exists somewhere in either one or both of the adjacent areas.

The following day, we get the other statement, which says:
"There is nothing which belongs jointly to both Spain and Portugal."
This means there's nothing in the overlapping area of the S and P circles, so we shade it out:

Okay, we've followed the information step by step.  But wait!  There's something wrong with this picture.  Note that the cross-border mark indicates that there might be something in the overlapping area, even though the shading indicates that there's nothing there.  To correct this, we must remove the cross-border mark, and instead place an X in the unshaded portion of the S circle, to indicate the territories belonging to Spain, and to Spain only:

The only blank area remaining is that for things which belong to Portugal, and only to Portugal.  If we later receive a statement informing us that something does indeed belong to Portugal, we'll put an X in the unshaded portion of the P circle.  Or if instead we get information that there's nothing that belongs to Portugal, we'll shade out the rest of the P circle.

Now we've diagrammed each of the four types of categorical statements—I, O, E, and A—plus one with an unspecified predicate category, and four showing various possibilities for two alternative predicate categories, using the techniques we've learned so far.  These techniques should cover virtually all diagramming issues involving only two terms, even if we encounter multiple (but non-conflicting) claims about those terms.  We haven't by any means exhausted all possibilities of two-category Venn diagram patterns, but the A, E, I, and O types, and combinations thereof, are the ones we'll most often encounter in categorical logic.

▼

WELCOME TO THE UNIVERSE! | USING A VENN DIAGRAM | ADDING ANOTHER CATEGORY | UNDISTRIBUTED MIDDLE FALLACY | TERMS

ADDING ANOTHER CATEGORY

Now we're ready to add another category to our universe.  When we do, we'll find that the number of distinct areas increases, from four to eight.  Again using colors to identify these areas, the blue, yellow, and red areas are the unshared portions of each of the three categories.  The violet area is the shared region of the blue and red circles; the green area is the shared region of the blue and yellow circles; and the orange area is the shared region of the red and yellow circles.  The central gray area is the region shared by all three circles, and the white area is the portion of the universe outside all of these categories.

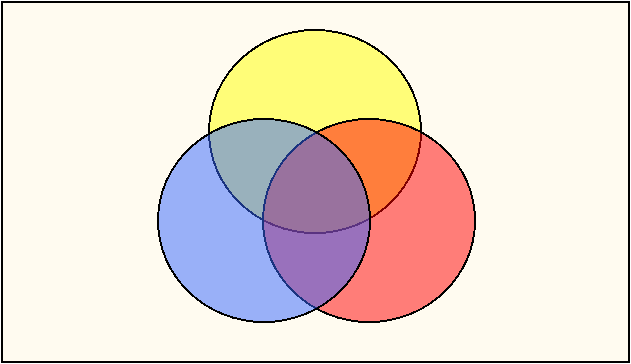
Venn stopped at three categories, because that's the largest number of both partially and fully overlapping yet distinct categories that can be diagrammed in two dimensions using only circles.  In a three-dimensional medium, using spheres instead of flat circles (each sphere centered at one of the four corners of a tetrahedron, also called a three-sided pyramid), a fourth sphere could be merged with the other three, and several more areas of overlap would appear.  In two dimensions, more categories could be diagrammed, but only if some of them are given odd shapes.  The addition of a fourth category would increase the number of distinct areas from eight to sixteen (including the external universe).  But in any case, clarity would suffer, and the intuitive information-conveying advantage of a simple diagram would be lost.

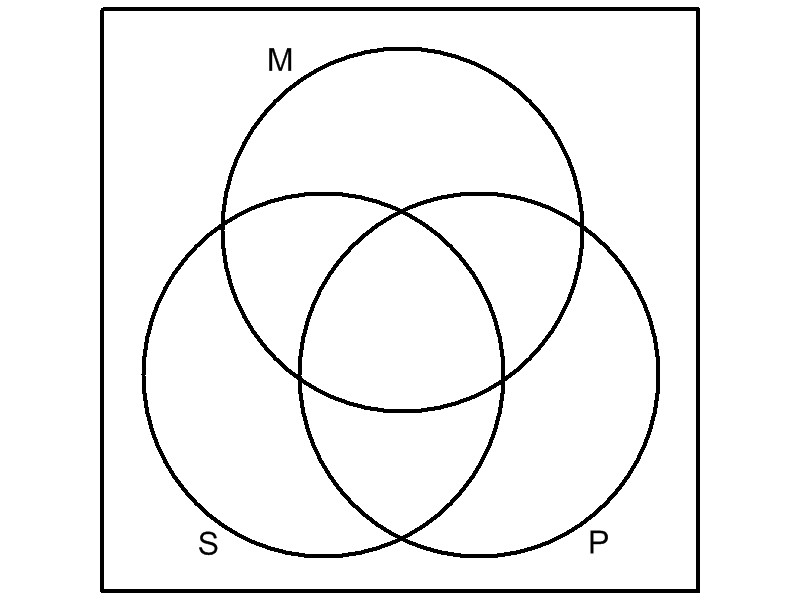
Even so, a three-category universe offers plenty of logical possibilities—in part because it's ideal for depicting the classic three-term syllogism.  The subject and predicate terms are those of the conclusion.  The remaining category is the syllogism's middle term, represented by the top-center circle.

IMPORTANT: When using a Venn diagram to illustrate a syllogism, we diagram the premises only, not the conclusion.  Our purpose is to use the diagram to see whether or not the premises actually do imply the conclusion, without presupposing it.  After we diagram the premises, we observe whether the markings on the completed diagram correspond to the conclusion.  If they do, then the syllogism is valid; if not, then the syllogism is invalid.

Let's try this syllogism for a start:

All artists are eccentric.
Some painters are artists.
So, some painters are eccentric.

The third statement is the conclusion; its subject term is "painters," and its predicate term is "eccentric."  As with the two-category diagrams, the conclusion's subject term corresponds to the S category in the three-category diagram, and its predicate term corresponds to the P category.  Thus, we would expect the conclusion, "Some painters are eccentric," to be represented in the completed Venn diagram by something—indicated by either a cross (x) or a cross-border mark—somewhere in the overlap area between the S and P circles.  We'll make a mental note of this for now, and we'll see if this turns out to be the case once we diagram the two premises.

The first premise also contains the predicate term of the conclusion, "eccentric," so this must be the major premise.  The second premise contains the conclusion's subject term, so this must be the minor premise.  In addition, the major and minor premises share the term "artists," so this is the middle term, which corresponds to the M category.

So now we must figure out which areas of the diagram are occupied by something, and which must be vacant.  Universal statements (forms A and E) tend to narrow down the range of possibilities more than particular statements (forms I and O), so beginning with a premise that's a universal statement is usually the quickest way to fill in a diagram without having to do any backtracking.

First, the only universal statement in this syllogism is the major premise, "All artists are eccentric."  "Artists" is the middle term.  It indicates that anything that isn't eccentric isn't an artist, so we shade out all parts of the M circle that don't overlap the "eccentric" category, which, as we've said, is the P circle.

Second, to account for the minor premise, "Some painters are artists," we look for any areas in the "painters" category (the S circle) which overlap the "artists" category (the M circle).  We find there are two of these; however, one of them is already shaded out, and thus vacant.  There's only one such area—the central region—which hasn't been eliminated from consideration, so we place an x there.  And indeed, the location of the x in the S-P overlap area reaffirms the conclusion, "Some painters are eccentric."  (The syllogism doesn't tell us anything about painters who aren't artists—i.e., whether they are or aren't eccentric—so we can neither mark nor shade out any area outside the M [artists] category.)

This is a pattern associated with a syllogism with a mood of AII (i.e., the major premise is an A-form statement, and the minor premise and conclusion are I-form statements).

[Incidentally, when dealing with mood, which is specified by a three-letter code corresponding to the A, E, I, or O forms of the syllogism's major and minor premises and its conclusion, respectively, it's important to remember that, in some text fonts, the upper-case letter I (i) closely resembles a lower-case L (l).  Be careful not to confuse the mood AII (AII) with the word All (All).]

NOTE: The remainder of this panel deals largely with various configurations of form, mood, and figure.  The discussion can get rather dry, and some readers might find their eyes glazing over.  This is okay.  Don't try to memorize everything.  The important thing is to become aware that some configurations are valid and some are not.  In most cases, the distinction between validity and invalidity, if not immediately obvious, requires just a little close examination and thinking-through of the syllogism,  This is where knowing how to use Venn diagrams as a visual aid to categorical reasoning can be extremely helpful.

For three-statement syllogisms, each of whose statements might take one of four forms, there are 4³ (4 ´ 4 ´ 4), or 64, possible moods.  Further complicating the matter is an additional factor called figure, which has to do with the sequence of major (P), minor (S), and middle (M) terms in each of the premises.  (While the sequences in the premises can vary, the sequence in the conclusion is always the minor term as subject and the major term as predicate.)  This gets a bit deeper into the topic than most people want or need to go, so we won't bother to discuss it in detail.  However, we'll list the four figures for any readers who might be interested.

Figure		Major Premise		Minor Premise		Conclusion
1st		M - P		S - M		S - P
2nd		P - M		S - M		S - P
3rd		M - P		M - S		S - P
4th		P - M		M - S		S - P

So, multiplying the 64 possible moods by the 4 figures, we get a total of 256 possible configurations of terms in a syllogism.  However, as we'll be relieved to learn, it turns out that all but twelve of these are invalid!  Moreover, the rules for Venn diagrams apply only to the modern system (in which the possibility of an empty category exists), and this further reduces the diagrammable number of valid configurations to eight.  (Not so bad after all!)

The only mood that is valid in all figures is EIO:

Figure		Pattern of Premises in EIO Mood
1st		No M are P, and some S are M, so some S are not P.
2nd		No P are M, and some S are M, so some S are not P.
3rd		No M are P, and some M are S, so some S are not P.
4th		No P are M, and some M are S, so some S are not P.

Let's take a look at how this mood appears in a Venn diagram, using the first-figure sequence.  If we'd like a concrete example, this one will do:

No shales are limestones.
Some fossil-bearing rocks are shales.
So, some fossil-bearing rocks are not limestones.

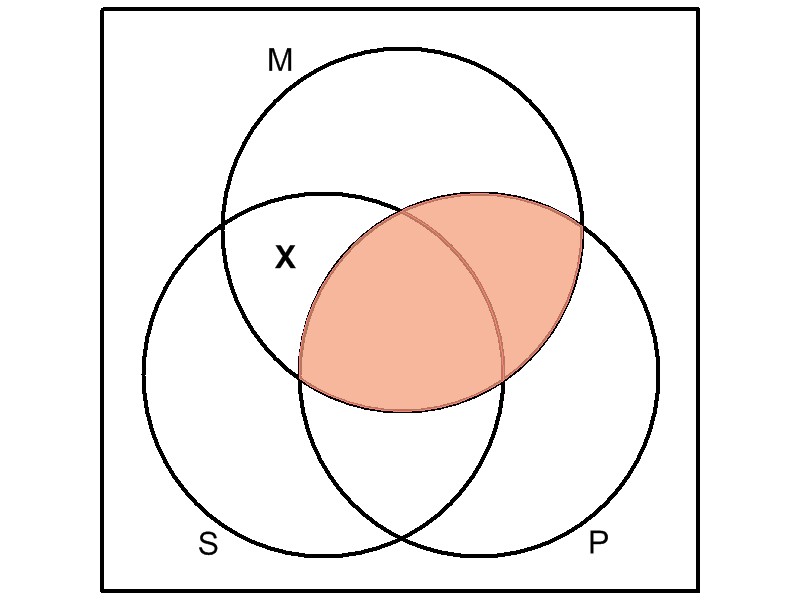
The major premise, "No M are P," requires us to shade out any areas where the M (shales) and P (limestones) circles overlap.  The minor premise, "Some S are M," is marked by placing an x in the only remaining area where the S (fossil-bearing rocks) and M (shales) circles overlap.  Since this occupied area isn't shared by the P (limestones) circle, the conclusion, "Some S (fossil-bearing rocks) are not P (limestones)," is visually affirmed.

Other moods that can be valid (depending on figure) are: AAA, AEE, AII, AOO, EAE, IAI, and OAO.  Some additional moods, which are invalid by modern standards, but which can be valid under the Aristotelian system are: AAI, AEO, and EAO.  From this, if we're observant, we can detect some general points which might come in handy at some juncture.

• A valid conclusion can be argued only if at least one of the premises is a universal (A or E) statement.

• A valid conclusion having a universal form (A or E) can be argued only from all universal premises (moods AAA, AEE, and EAE).

• A particular (I or O) conclusion argued from two universal (A and / or E) premises can be valid only under the Aristotelian (no-empty-categories) system.

We won't bother to diagram all twelve potentially valid moods, nor even just the eight that modern thought accepts.  But let's try one more, to demonstrate a pattern produced when both premises are universal statements:

All whales are mammals.
No mammals are fish.
So, no whales are fish.

First, we identify each statement's function in the syllogism.  The conclusion is "no whales are fish;" the subject term is "whales" and the predicate term is "fish."  This time, the premise that contains the conclusion's predicate term is the second one, "No mammals are fish," so this is the major premise.  But to determine the syllogism's logical configuration, we need to consider the statements according to the standard form—major premise, minor premise, and conclusion, in that order.

No mammals are fish.
All whales are mammals.
So, no whales are fish.

The major premise is an E statement; the minor premise has an A form; and the conclusion is another E form.  So this syllogism has mood EAE, and we'd expect the diagrammed pattern to be different from the AII and EIO syllogisms we diagrammed before.  Let's see.  The subject term is "whales," the predicate term is "fish," and the middle term is "mammals."  Since both premises are universal, let's just diagram them in order.

The major premise relates the middle term "mammals" to the predicate term "fish," declaring them mutually exclusive.  So, we begin by shading out (in red) the overlapping areas between the middle and predicate categories, to mark this region as vacant.

The minor premise relates the subject term "whales" to the middle term "mammals," with a claim that all members of the category of whales are also in the category of mammals.  In other words, there are no whales that are not mammals.  So, we shade out (in blue) any areas of the subject category (whales) that don't overlap the middle category (mammals).

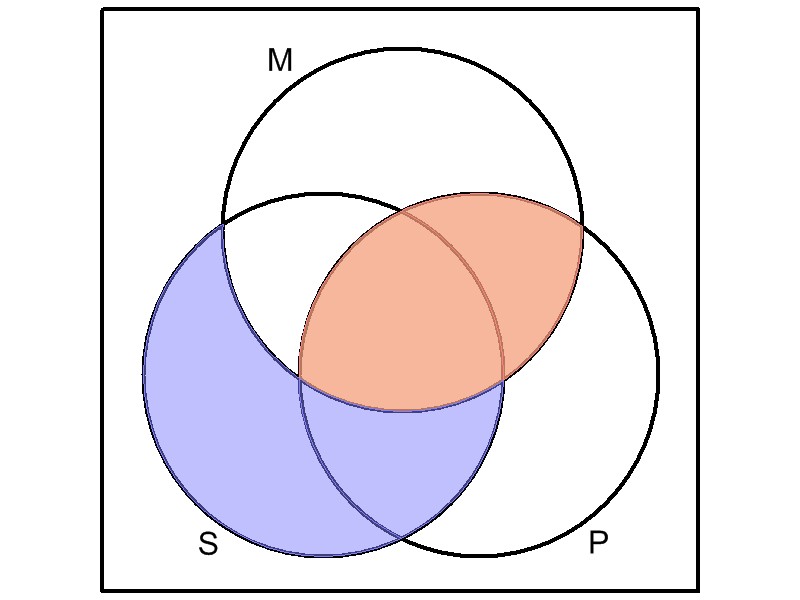
From the completed diagram, we can visually observe that the only potentially occupied area of the "whales" category (the S circle) is the unshaded portion that overlaps the "mammals" category (the M circle) but not the "fish" category (the P circle).  Since both of the premises of this syllogism are universals, the only areas marked are those which are ruled out as unoccupied.

Like most people, Aristotle would have reasoned that, if there is such a thing as all whales, then surely some whales must exist in the remaining presumably non-vacant portion of the S circle.  But Venn, being a modern thinker who accepts zero as a possible value for all, does not make such an assumption.  Lacking a clear stipulation that some whales exist, we can't jump to the conclusion that there must be whales in the remaining portion of the S circle.

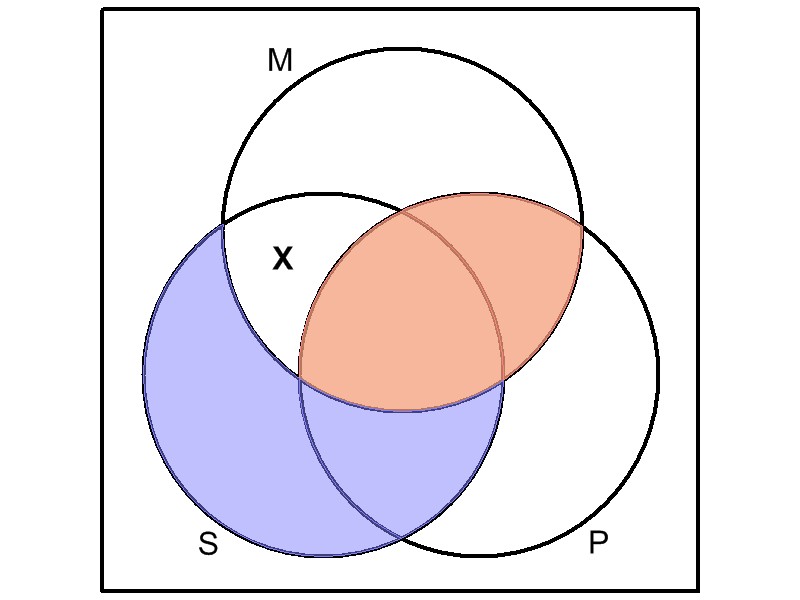
But suppose that, besides the syllogism, we have additional information that at least one whale exists.  All whales must occupy the S circle, and they can occupy only an unshaded, non-empty area.  There's only one area in the diagram that satisfies both requirements: where the S (whales) circle overlaps the M (mammals), but not the P (fish).  So, that's where we place the X.  And indeed, this corresponds to the conclusion, "No whales are fish."  Other unshaded areas might or might not have things in them, but those things are not whales.

---

HINT: If you find yourself using lots of Venn diagrams as aids to thinking or communication, consider creating a printable page of blank diagrams (rectangle and circles only, with no shading or occupancy markings) to use as a handy template.  If you wish, you may use the following sample as a prototype.  Highlight and copy the entire contents of the box below, and insert / paste it into a word-processor page, with margins set to 0.5 inches (1.27 cm.).  Then save the file, and print it to use as a sketch sheet in your projects.

Subject: ____________________________________  S = ________________________________________ M = _______________________________________ P = ________________________________________ Valid?   Yes / No (circle one)	Subject: ____________________________________  S = ________________________________________ M = _______________________________________ P = ________________________________________ Valid?   Yes / No (circle one)
Subject: ____________________________________  S = ________________________________________ M = _______________________________________ P = ________________________________________ Valid?   Yes / No (circle one)	Subject: ____________________________________  S = ________________________________________ M = _______________________________________ P = ________________________________________ Valid?   Yes / No (circle one)

▼

WELCOME TO THE UNIVERSE! | USING A VENN DIAGRAM | ADDING ANOTHER CATEGORY | UNDISTRIBUTED MIDDLE FALLACY | TERMS

FALLACY OF THE UNDISTRIBUTED MIDDLE

No, this isn't about middle-age waistline expansion, or a tendency of middle-class folks to cluster in groups.  The "middle" in question here is the middle term of a categorical syllogism.  Syllogisms, as we're now aware, are governed by strict rules.  But even though the rules are fairly simple, they aren't generally understood by most people.  Besides, there are many other things to keep in mind while working our way through a complex line of reasoning.  Thus, it isn't surprising that things sometimes go wrong.

One such problem occurs when the middle term of a syllogism is undistributed.  A term is said to be distributed in a statement if the statement says something about every member of the category specified by the term.  If the statement doesn't say something about every member of the term's category, the term is undistributed in that statement.  However, if a term is distributed in at least one premise of a syllogism, then it is effectively distributed for the entire syllogism.  To put it another way, a term that is not distributed in at least one premise of a syllogism is undistributed for the syllogism as a whole.  And if this undistributed term is the middle term of a syllogism, then a fallacy has occurred and the syllogism is invalid.  So, if we're working on a case for which we want the reasoning to be air-tight, we need to be aware of where the leaks are most likely to occur.  So far as syllogistic structure goes, this is most simply explained in terms of a statement's form.

• A-form (All S are P):  The subject term S is distributed by the word all (or an equivalent, e.g., every or each), while its predicate term P is not.

• E-form (No S are P):  Both the subject term S and the predicate term P are distributed, because not only does "No S are P" say something about all S, it also implies "No P are S," which states something about all P.

• I-form (Some S are P):  Neither term is distributed.

• O-form (Some S are not P):  The subject term S is not distributed, but the predicate term P is.  Why this last is so might at first seem obscure; but the statement claims, in effect, that all P is excluded from part of the category of S.

Now, it's a requirement of categorical syllogisms that the middle term must be distributed in at least one of the two premises.  So if, for example, a syllogism's middle term happens to end up in the subject term of an O-form major premise, and also in the predicate term of an A-form minor premise—or some other combination in which it fails to be distributed by either premise—we end up with a fatal gap in the flow of logic, as in...

Some carnivores are cats.
All dogs are carnivores.
So, some dogs are cats..

Note that neither of the premises makes a universal claim about all (or no) carnivores (the middle term), so the middle term is undistributed.  Thus, there is no logical connection to connect dogs directly to cats, except that all dogs and at least some cats share the category of carnivores.  The premises provide no justification for concluding that any dog is a cat, let alone that all dogs are cats.  If the major premise were "All carnivores are cats," then a conclusion that all dogs are cats would be logically (if not factually) justified.  But the fact that there is no such universal premise about the middle term, carnivores, leaves us with no way to justify this or any other conclusion from this particular pair of premises.

Here's another example of a syllogism with an undistributed middle term:

Some religious people are not Protestants.
All Lutherans are religious people.
So, some Lutherans are not Protestants.

Here the middle term is "religious people."  And we see that neither premise makes any implication about all (or no) religious people, thus leaving the term undistributed.  Let's examine this syllogism in the form of a Venn diagram.  The conclusion indicates that "Lutherans" is the subject term, and that "Protestants" is the predicate term.  In this instance, the first premise is a particular statement, which tells us where something is in the diagram.  The second premise is a universal statement, which tells us where something isn't, and thus should be diagrammed first, in the interest of narrowing down the possibilities.

"All Lutherans are religious people" tells us that there are no Lutherans who aren't religious; so we shade out all portions of the Lutherans (S) circle that don't overlap the religious people (M) circle.  These include the non-overlapping portion of the S circle, as well as the part of the S circle that overlaps the P circle only.  Now, "Some religious people are not Protestants" tells us to consider as potentially occupied all unshaded areas of the religious people (M) circle that do not overlap the Protestants (P) circle.  These would be the non-overlapping portion of the M circle, as well as the part of it that overlaps the S circle but not the P circle; so, we place a cross-border marker across the arc separating these two areas.

To avoid confusion when discussing the various areas, let's number each distinct area in the diagram, and provide a brief description of each numbered area.  Bear in mind, of course, that the numbers are for identification only; they do not signify that anything occupies an area.

	area	terms	contents
	1	universe	everything else
	2	S-only	Lutheran
	3	S+P	Lutheran & Protestant
	4	P-only	Protestant
	5	P+M	Protestant & religious
	6	M-only	religious
	7	S+M	Lutheran & religious
	8	S+P+M	Lutheran & Protestant & religious

Now, mentally picture what the conclusion would indicate on the diagram: "Some Lutherans are not Protestants" tells us that there ought to be something occupying an unshaded portion of the S circle that doesn't overlap the P circle.  There's only one area that comes close to satisfying these requirements: what we've identified as area 7, which is the overlap of S (Lutheran) and M (religious) circles, but excluding the P (Protestant) circle.

But there's a problem here:  There's no X to indicate that area 7 is definitely occupied.  There's only a cross-border mark between area 7 and area 6 (religious only).  While this mark indicates that at least one of these two areas is occupied, it doesn't specify which is actually occupied.  If we had particular information that the S-M overlap area 7 is occupied (e.g., "Some religious people are Lutheran but not Protestant"), that would answer the question directly.  Or if we had information that the M-only area 6 is empty (e.g., "All religious people are either Lutheran or Protestant"), we could conclude that all occupying things indicated by the cross-border mark must be in the S-M overlap area 7.  But the syllogism's premises don't provide such information.¹  Consequently, we can't conclude from the premises that the religious-Lutheran-non-Protestant area has anything in it.  So again, the premises of this syllogism do not give rise to its proposed conclusion, and the syllogism is thus invalid!

The "undistributed middle term" is among that relatively small group of less than obvious but nonetheless deadly fallacies classified as formal errors.  In some instances, the result is a jaw-dropper.  In others, the error can slip by unnoticed—but it's no less fatal to the chain of reasoning.

---

NOTES ON THIS TOPIC

1. In real life, we know of many sects which are neither Lutheran nor Protestant—Muslims, Jews, Hindus, and Buddhists, in addition to non-Protestant Christians such as Catholics and Copts, just to name a few.  But even if we could use this information to show that area 6 is occupied, it still wouldn't tell us anything about whether there's anything in area 7.  Only knowledge that area 6 is empty (which is obviously not actually the case) would tell us that everything that occupies either area 6 or area 7 must all be in area 7.

▼

WELCOME TO THE UNIVERSE! | USING A VENN DIAGRAM | ADDING ANOTHER CATEGORY | UNDISTRIBUTED MIDDLE FALLACY | TERMS

TERMS

• subject term / category

• predicate term / category

• middle term / category

• mood

• figure

• fallacy of undistributed middle term

This has been the final lesson in the logic portion of this on-line course.  You now have the choice either to continue with a final section on ethics, which also functions as a demonstration and practical exercise for applying logical thinking, or to end your participation in the course.  If you prefer not to continue, please visit the Wrap-up page for parting thoughts.  In any case, we congratulate you on your progress, and appreciate your participation.

►  Next: A Rational Ethic (practical exercise)

► Finish: Wrap-up

WELCOME TO THE UNIVERSE! | USING A VENN DIAGRAM | ADDING ANOTHER CATEGORY | UNDISTRIBUTED MIDDLE FALLACY | TERMS

▲